WQU with Path Compression

• Review of Weighted Quick Union
• Path Compression
• Proof of amortized \(O(\log^{\ast}{n})\) find for WQU-PC
  • Two Properties
    • (1) For every element \(e\), \(rank(e) > rank(e\text{.parent})\)
    • (2) If there are \(n\) elements, there are at most \(n/2^k\) elements of \(rank = k\)
  • Amortization
    • Bounding \(E(n)\)
    • Bounding find
  • Corollary: Amortized \(O(\log^{\ast}{n})\) union

Review of Weighted Quick Union

A WQU data structure lets us efficiently represent and interact with disjoint sets. Given \(n\) elements, which start off as \(n\) one-element sets, we can call union on any two elements to union the two sets they belong to. Weighted quick union gives us a runtime bound of \(O(\log{n})\) for any call to union. This is due to the weighted component of the algorithm: the union will always make the set with a less elements a child of the set with more elements. See the below image (taken from this page):

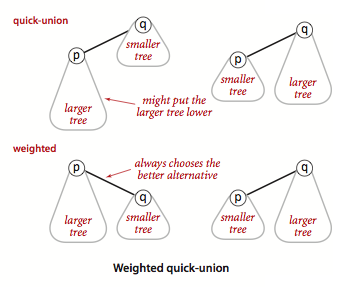
The only way to increase the height of a set’s tree representation is if you union two sets with the same number of elements (try to draw a few examples and visualize this). As a result, the upper bound on the height of a set’s tree is \(\log{n}\). To end up with a tree with height \(\log{n}\), pairwise union all equal-sized sets, and do this \(\log{n}\) times. Each time you union two equal-sized sets, the height of the resulting set is increased by \(1\), so the tree at the end has height \(\log{n}\). See below for \(n = 8\):

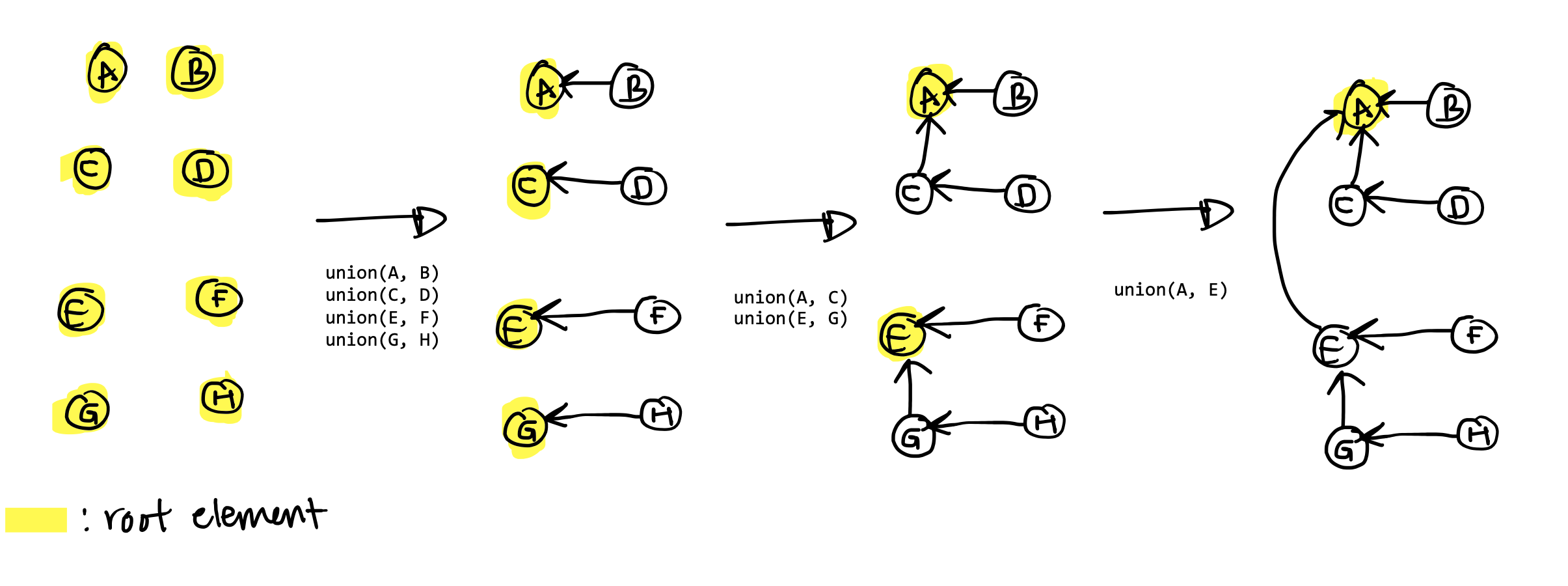
This means the bound on the runtime of calling find, which finds the root of a set based on an element, is \(O(\log{n})\), since an element at the bottom of the tree would have to traverse the entire height of the tree to reach the root.

To make find asymptotically faster, we will use path compression every time we call find.

Path Compression

Here is the pseudo-code of find with path compression:

def find(el):
    if el is not the root:
        el.parent = find(el.parent)
    return el.parent

This above pseudo-code is quite dense, try to work through it. Path compression takes all the nodes in the path traversed (starting at el and ending at the root) and makes each node a child of the root (hence, it is compressing the path). Here is an example:

     A
   / | \
  B  C  D
    / \
   E   F
  / \
 G   H

Calling find(G) will transform the tree to become this:

       A
  / / |  | \ \
 B C  E  D  E G
  /   |
 F    H

(C and E got moved up to be children of the root).

The key insight to why path compression gives a better runtime for \(m\) calls to find (if \(m >> n\)) is because everytime you call find, you do some work that flattens the tree, and ultimately gives find an amortized runtime of \(O(\log^{\ast}{n})\).

Proof of amortized \(O(\log^{\ast}{n})\) find for WQU-PC

The iterated logarithm, \(\log^\ast n\) is defined as the number of times you apply \(\log\) until you get \(\leq 1\). For example, \(\log_2^\ast2^{2^2} = 3\). \(\log^\ast\) grows very slow, see the below example for some intuition why:

In general, an algorithm with time complexity \(\log^\ast n\) would be very fast as \(n\) grows larger (just below constant time!), so this is quite desirable.

First, let’s define the \(rank\) of a root to be the height of its underlying tree. Before any union calls are made, each element, which is the root of its own one-element set, has \(rank = 0\). When we union two sets with equal \(rank\), we increment the root of the unioned set’s \(rank\) by \(1\), because the underlying tree has had its height increased by \(1\).

I will use “root” and “tree” interchangeably, so when I say a “the number of elements in a root of \(rank = k\)”, I really mean “the number of elements in the tree that has a \(rank = k\) root”.

Two Properties

Here are two useful properties of \(rank\) that will be used in our proof later:

(1) For every element \(e\), \(rank(e) > rank(e\text{.parent})\)

If \(rank(e) = k\), that means it was created by unioning two elements whose sets had \(rank = k-1\).

(2) If there are \(n\) elements, there are at most \(n/2^k\) elements of \(rank = k\)

An important observation: elements that are no longer roots still have a \(rank\) because in the beginning, they started out as roots of their own one-element set. Note that their \(rank\) can no longer increase once they become a child of another root.

First, let’s prove that a root with \(rank = k\) has at least \(2^k\) elements.

The total number of elements \(T(k)\) for a root of \(rank = k\) is something we can lower bound. \(T(k)\) is at least the sum of the number of elements in the two equal-ranked trees that were merged. Observe that this is a lower bound because you could always increase the number of elements without increasing the rank by unioning in more roots with \(rank < k\).

Expanding and simplifying \(T(k)\):

This means that if we have \(n\) elements, there are at most \(n/2^k\) elements of \(rank = k\), since each root with \(rank=k\) has at least \(2^k\) elements. This means the highest possible \(rank\) is \(\log n\) since there is at most one root with \(2^{\log n} = n\) elements.

Onto the proof…

Amortization

What we’re going to try prove is that for a call to find, the time complexity is \(O(\log^\ast n)\). Some calls to find might take some extra work, but we will be able to bound the total amount of extra work \(E(n)\) over all calls to find as a function of the number of elements (\(n\)).

We will then show that if you \(m\) calls to find, \(E(n)\) becomes negligible when \(m >> n\), . This is the soul of amortization.

According to (2), the possible range of ranks an element could have is \([0, \log n]\). Let’s divide this range of non-zero ranks into the following groups:

Each group has the form \(\{r + 1, r + 2, \ldots, 2^{r}\}\). In total, there are \(\log^{\ast} n\) groups.

Bounding \(E(n)\)

Recall in (2) that once an element is no longer a root, it’s rank can no longer increase. We will give each child element with \(rank = k\) the ability to take \(2^r\) total extra steps over all calls to find, where \(r\) is the first value of the group that \(k\) falls in.

Claim: The total amount of extra steps we give is at most \(n\log^\ast n\). That is, \(E(n) \leq n\log^\ast n\).

Proof: Child elements with \(rank = k\) that are in the group \(\{r + 1, r + 2, \ldots, 2^{r}\}\) each get \(2^r\) extra steps. From (2) we can upper bound the total amount of child elements with a rank in that group:

For each group, the total amount of extra steps given is at most \(n\), and there are \(\log^\ast\) groups.

Bounding find

We will define the amount of work done by find(e) as the length of the path between e and the root. Consider the elements \(x\) in this path, ranks ascending (see (1)). Each element \(x\) has \(rank = r_x\). Each element’s parent \(x\text{.parent}\) has a \(rank = r_p\) that is either in a larger group or the same group as \(r_x\).

Two observations:

1. At most \(\log^\ast{n}\) elements would have parents with a rank in a larger group. (Why? That’s how many groups there are.)
2. If \(x\text{.parent}\) has a rank that is in the same group as the rank of \(x\), \(x\) will use one of its allocated extra work steps.

Observation 1 implies a \(O(\log^{\ast}n)\) time complexity of find if we can prove that each child element does not spend more work steps than it was allocated.

Every time a child element uses one of its extra work steps, it’s parent becomes one with a higher rank (path compression changes its parent). A child element needs at most \(2^r\) extra steps to change to a parent that has a rank in a higher group. Once its parent’s rank is in a higher group, it does not need any more extra steps because of Observation 1.

The total time complexity of \(m\) calls to find on \(n\) elements is:

At last, we have proved that the amortized runtime of find is \(O(\log^\ast n)\).

You can prove an even tighter upper bound, see this paper for more.

Corollary: Amortized \(O(\log^{\ast}{n})\) union

Since union’s time complexity depends on find, union also has an amortized runtime of \(O(\log^\ast n)\).