Discussion 03 Guide
Question 2
a) Suppose you have access to function \(R\) that takes a 128-bit seed \(s\) and integers \(n\), \(m\) as input. \(R\) outputs the \(n\)th (inclusive) through \(m\)th (exclusive) bits produced by the a pseudorandom generator \(PRNG\) when it is seeded with seeds.
\[RNG(s, n, m) = PRNG(s)[n:m]\]Use \(R\) to make a secure symmetric-key encryption scheme. That is, define the key generation algorithm, the encryption algorithm, and the decryption algorithm.
Our inspiration for this algorithm comes from the one-time pad. A one-time pad is secure, as long as the key is never reused in an encryption. We can source a key for the encryption of each message from \(RNG\) with \(S\) being our key (\(s = K\)). Let \(M\) be a 128-bit padded message. Our scheme is as follows:
- Key Generation. Set \(K \leftarrow_R \{0, 1\}^{128}\) (a random 128-bit number).
-
Encryption. We can prevent reuse of one-time pad keys by keeping track of the random numbers we have consumed from \(RNG\) with a variable \(j\).
\[Enc(K, M) = RNG(K, j, j+128) \oplus M || j\]Here, \(||\) means concat, and we need to concat \(j\) to our ciphertext for decryption. We also increment \(j\) by \(128\) after each encryption so our RNG gives us fresh random bits.
-
Decryption. Remember \(x \oplus x = 0\). Let \(\hat{C}\) be the ciphertext from \(Enc\).
First, unpack \(j\) from \(\hat{C}\).
\[C, j = \hat{C}_{0, \ldots, 127}, \hat{C}_{128}\] \[\begin{align} Dec(C, j, K) &= RNG(K, j, j+128) \oplus C \\ &= RNG(K, j, j+128) \oplus RNG(K, j, j+128) \oplus M \\ &= 0 \oplus M \\ &= M \end{align}\]
b) Explain how using a block cipher in counter (CTR) mode is similar to the scenario described above.
Below is the algorithm for CTR mode:
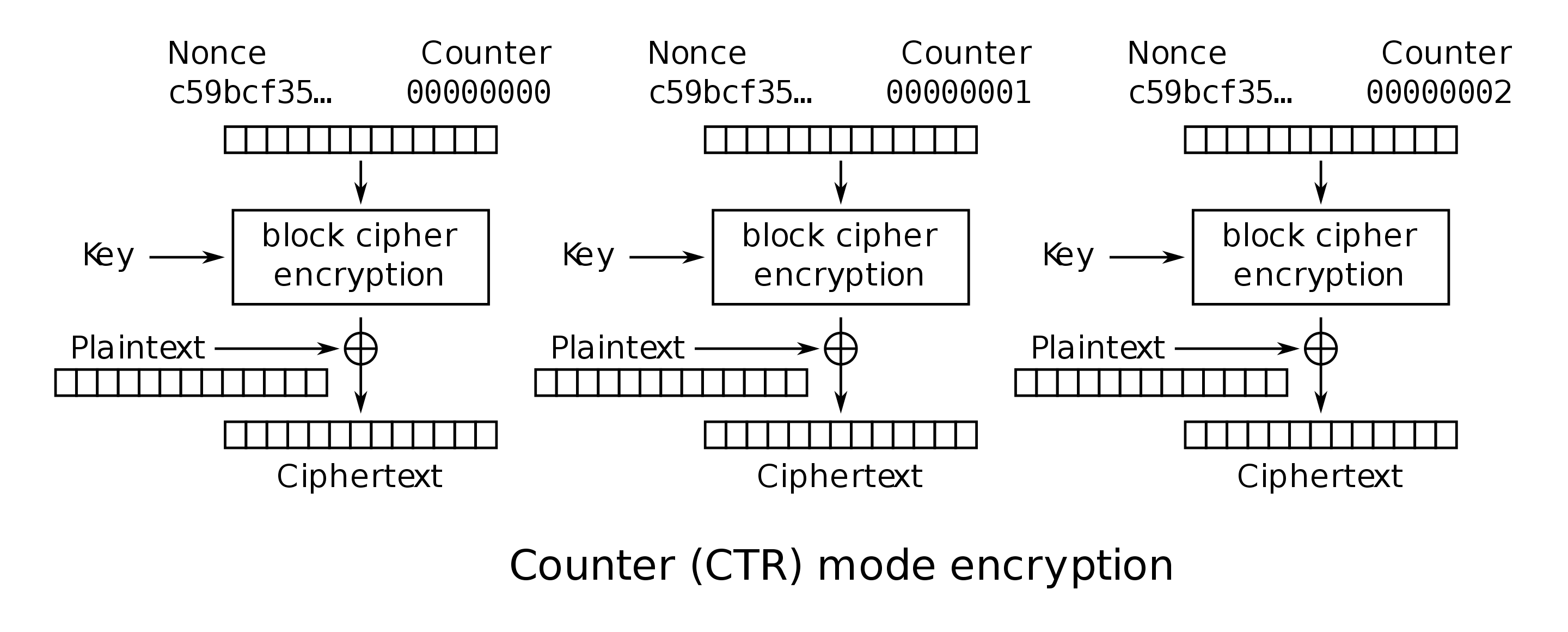 There is a nonce (random number, also known as the initialization vector)
that gets encrypted by a block cipher, producing a key for a one-time pad.
The reason we have this nonce is that it makes the encryption
non-deterministic as long as the nonce is used once per encryption.
This is similar to the scheme above because we never reuse bits from
\(PRNG\).
There is a nonce (random number, also known as the initialization vector)
that gets encrypted by a block cipher, producing a key for a one-time pad.
The reason we have this nonce is that it makes the encryption
non-deterministic as long as the nonce is used once per encryption.
This is similar to the scheme above because we never reuse bits from
\(PRNG\).
One advantage of CTR mode is that, unlike our scheme, its computation can be easily parallelized because each partition’s encryption can be computed independently, given a nonce and a counter. Our scheme requires keeping track of \(j\) across all encryptions, and also needs one bit from the PRNG for every bit in the message.